Seconde loi de Kepler - La loi des aires
La seconde loi de Kepler fut publiée en 1609.
Si S est le Soleil et M une position quelconque d'une planète, l'aire balayée par le segment [SM] entre deux positions C et D est égale à l'aire balayée par ce segment entre deux positions E et F si la durée qui sépare les positions C et D est égale à la durée qui sépare les positions E et F. La vitesse d'une planète devient donc plus grande lorsque la planète se rapproche du Soleil. Elle est maximale au voisinage du rayon le plus court (le périhélie), et minimale au voisinage du rayon le plus grand (l'aphélie).
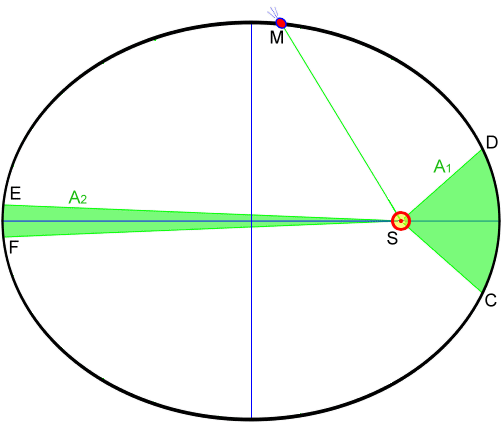
Dans le schéma précédent, les aires A1 et A2 sont égales. La durée de déplacement entre les points d'orbite C et D est donc égale à celle séparant E et F.
De cette deuxième loi, on déduit que la force exercée sur la planète est constamment dirigée vers le Soleil.
Soit A(t) l'aire de la surface balayée par le rayon vecteur 
durant le mouvement, alors cette seconde loi stipule que des aires égales sont balayées dans des temps égaux.
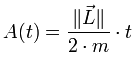
où :
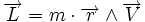est le moment cinétique relativement à l'origine où se trouve le Soleil.- m est la masse de la planète.
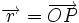est le vecteur allant du Soleil à la planète.
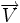est la vitesse de la planète.
Tags
Réagir
1 Commentaire
-
Cela ne s'applique donc pas à la lumière, vu que sa masse m est 0, et on obtient alors un dénominateur nul lors de l'équation.